2021. 2. 4. 22:58ㆍ알고리즘

문제
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
문제를 먼저 풀고 오시는 것을 추천합니다.
이 문제의 풀이는 DP(Dynamic Programming) 외에도 다양한 방법이 있을 수 있으며 제가 보여드리는 풀이는 그 중 하나입니다.
문제분석
정수 X에 사용할 수 있는 연산은 세가지입니다.
① 1을 뺀다. -> X가 어떤 수이든지 1을 뺄 수 있다.
② X가 2로 나누어 떨어지면, 2로 나눈다.
③ X가 3으로 나누어 떨어지면 3으로 나눈다.
실제 문제와 다르게 알아보기 쉽게 하기 위하여 1번은 1 빼기, 2번은 2로 나누기, 3번은 3으로 나누기로 재정리하였습니다.
정수 N이 주어졌을 때, 세 가지 연산을 적절히 사용해서 1을 만들 때 연산을 사용하는 횟수의 최소값을 출력해야 합니다.
입력
첫째 줄에 정수 N( 1<= N <= 1000000)가 주어집니다.
출력
연산을 하는 횟수의 최소값을 출력합니다.
풀이
DP는 점화식을 구하면 풀 수 있다고 합니다.
수학을 잘 하시는 분들은 점화식을 쉽게 구할 수 있겠지만 저는 수학을 잘 하는 편이 아니라서 점화식을 구하기 위하여 법칙을 찾아보려고 노력합니다. (점화식을 쉽게 구하시는 분들은 아마 이 정도의 문제는 검색도 안 하실 겁니다.)
일단 작은 수를 하나 정해서 법칙을 찾아보도록 하겠습니다.
정수 10이 주어졌을 때 10에서 연산을 해서 1까지 가는 최소 연산횟수를 구할 수 있지만
반대 방향으로 생각해보면 1부터 10까지 올라가는 연산을 할 수 있습니다.
사람이 직접 하는 계산이면 귀찮아서 모든 수를 계산하지 않겠지만 컴퓨터는 모든 수에 대해서 계산하면 쉽게 답을 찾을 수 있습니다. (다른 말로 완전탐색이라고 하지요.)
1 ~ 10 사이의 수를 i라고 가정하겠습니다.
i가 될 수 있는 연산횟수를 구해보도록 하겠습니다.
참고로 연산횟수는 최소값을 구해야 하므로 3가지 연산이 가능한 경우에는 가장 작은 횟수를 선택해야 합니다.
i 가 1일 때
1은 이미 1이기 때문에 연산이 필요없습니다.
따라서, 1이 될 수 있는 연산횟수는 0입니다. (초기값 설정)
아래 그림에 있는 배열은 연산횟수를 저장하는 배열(d 배열이라고 하겠습니다.)입니다.
그러므로 d[1] = 0 입니다.

i가 2일 때
i가 2일 때 i가 2로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ② 2 나누기입니다.
그러면 연산횟수는 2개 연산에 대해서 계산해보겠습니다.
아래 그림에서와 같이 ①번 연산은 i-1=2-1=1 연산횟수에서 1을 더합니다. d[2] = d[1] + 1 = 1
②번 연산은 i/2=2/2=1 연산횟수에서 1을 더합니다. d[2] = d[1] + 1 = 1
두 연산 중 어떤 것을 하더라도 d[2] = 1입니다.

i가 3일 때
i가 3일 때 i가 3으로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ③ 3 나누기입니다.
그러면 연산횟수는 2개 연산에 대해서 계산해보겠습니다.
아래 그림에서와 같이 ①번 연산은 i-1=3-1=2 연산횟수에서 1을 더합니다. d[3] = d[2] + 1 = 2
③번 연산은 i/3=3/3=1 연산횟수에서 1을 더합니다. d[3] = d[1] + 1 = 1
두 연산 중 ③번 연산이 더 작으므로 d[3] = 1이 됩니다.

i가 4일 때
i가 4일 때 i가 2로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ② 2 나누기입니다.
그러면 연산횟수는 2개 연산에 대해서 계산해보겠습니다.
아래 그림에서와 같이 ①번 연산은 i-1=4-1=3 연산횟수에서 1을 더합니다. d[4] = d[3] + 1 = 2
②번 연산은 i/2=4/2=2 연산횟수에서 1을 더합니다. d[4] = d[2] + 1 = 2
두 연산 중 어떤 것을 하더라도 d[4] = 2입니다.

i가 5일 때
i가 5일 때 i는 2나 3으로 나누어지지 않기 때문에 가능한 연산은 ① 1 빼기입니다.
①번 연산은 i-1=5-1=4 연산횟수에서 1을 더합니다. d[5] = d[4] + 1 = 3
그러므로 d[5] = 3이 됩니다.

i가 6일 때
i가 6일 때 i가 2나 3으로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ② 2 나누기, ③ 3 나누기입니다.
그러면 연산횟수는 3개 연산에 대해서 계산해보겠습니다.
①번 연산은 i-1=6-1=5 연산횟수에서 1을 더합니다. d[6] = d[5] + 1 = 4
②번 연산은 i/2=6/2=3 연산횟수에서 1을 더합니다. d[6] = d[3] + 1 = 2
③번 연산은 i/3=6/3=2 연산횟수에서 1을 더합니다. d[6] = d[2] + 1 = 2
최소값은 ②, ③ 연산 중 어떤 것을 하더라도 d[6] = 2입니다.

i가 7일 때
i가 7일 때 i는 2나 3으로 나누어지지 않으므로 ① 1 빼기만 가능합니다.
①번 연산은 i-1=7-1=6 연산횟수에서 1을 더합니다. d[7] = d[6] + 1 = 3
그러므로 d[7] = 3이 됩니다.

i가 8일 때
i가 8일 때 2로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ② 2 나누기입니다.
그러면 연산횟수는 2개 연산에 대해서 계산해보겠습니다.
아래 그림에서와 같이 ①번 연산은 i-1=8-1=7 연산횟수에서 1을 더합니다. d[8] = d[7] + 1 = 4
②번 연산은 i/2=8/2=4 연산횟수에서 1을 더합니다. d[8] = d[4] + 1 = 3
두 연산 중 ②번 연산이 더 작으므로 d[8] = 3이 됩니다.
i가 9일 때
i가 9일 때 i가 3으로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ③ 3 나누기입니다.
그러면 연산횟수는 2개 연산에 대해서 계산해보겠습니다.
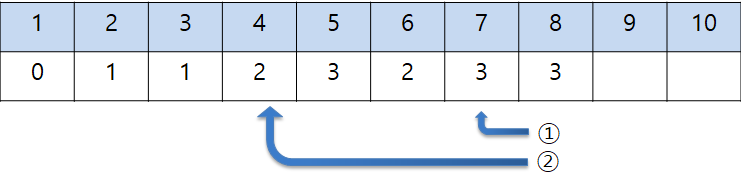
아래 그림에서와 같이 ①번 연산은 i-1=9-1=8 연산횟수에서 1을 더합니다. d[9] = d[8] + 1 = 4
③번 연산은 i/3=9/3=3 연산횟수에서 1을 더합니다. d[9] = d[3] + 1 = 2
두 연산 중 ③번 연산이 더 작으므로 d[9] = 2이 됩니다.
i가 10일 때
i가 10일 때 2로 나누어서 나머지가 0이 되므로 가능한 연산은 ① 1 빼기와 ② 2 나누기입니다.
그러면 연산횟수는 2개 연산에 대해서 계산해보겠습니다.
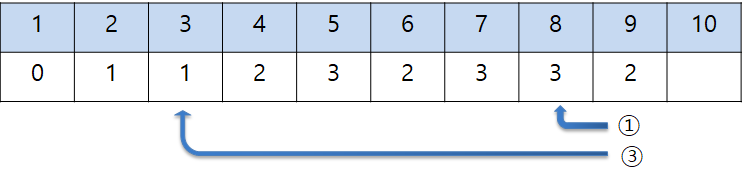
아래 그림에서와 같이 ①번 연산은 i-1=10-1=9 연산횟수에서 1을 더합니다. d[10] = d[9] + 1 = 3
②번 연산은 i/2=10/2=5 연산횟수에서 1을 더합니다. d[10] = d[5] + 1 = 4
두 연산 중 ①번 연산이 더 작으므로 d[10] = 3이 됩니다.

d[10] 값이 3이므로 10이 1로 될 때까지 진행하는 연산은 3번입니다.
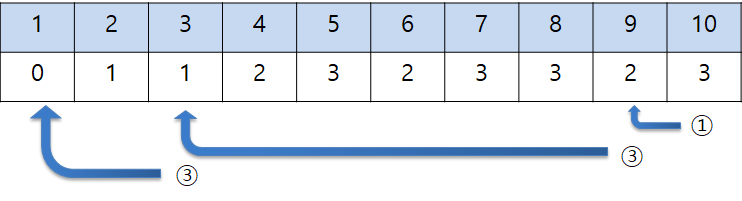
위에서 풀은 걸 10부터 1까지 작은 수가 되는 경우를 찾아보면
10 -> 9(1 빼기) -> 3(3 나누기) -> 1 (3 나누기)로 이동하는 것을 알 수 있습니다.
점화식 및 소스
무식하게 하나씩 해보았지만 법칙이 보인다는 걸 알 수 있습니다.
최소 연산횟수를 저장하면 다시 계산할 필요가 없습니다. (메모이제이션)
- 1를 뺄 때는 d[i] = d[i-1] + 1
- 2로 나눌 수 있을 때는 d[i] = d[i/2] + 1
- 3으로 나눌 수 있을 때는 d[i] = d[i/3] + 1
소스로 구현하실 때 초기값인 d[1] = 0도 잊지 마시길 바랍니다.
지금 같은 경우는 굳이 안 넣어도 0으로 설정되지만 다른 DP 문제를 풀 때 초기값을 설정하는 습관이 있어야 실수하지 않습니다.
import java.util.Arrays;
import java.util.Scanner;
public class Main
{
static int d[];
public static void main(String[] args) throws Exception
{
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
d = new int[N+1];
d[1] = 0;
for (int i = 2; i < N+1; i++)
{
d[i] = d[i-1]+1;
if (i % 2 == 0 && d[i] > d[i/2]+1)
{
d[i] = d[i/2]+1;
}
if (i % 3 == 0 && d[i] > d[i/3]+1)
{
d[i] = d[i/3]+1;
}
}
System.out.println(d[N]);
// N까지의 연산횟수 출력
// System.out.println(Arrays.toString(d));
}
}
관련글:
2020/12/10 - [Algorithm] - [알고리즘] 백준 온라인 저지 사이트 소개
[알고리즘] 백준 온라인 저지 사이트 소개
삼성 소프트웨어(SW) 테스트 또는 SW검정을 준비하시는 분들을 위하여 알고리즘 관련 내용을 포스팅하려고 합니다. 알고리즘을 공부하면 내가 만든 소스가 맞는지 확인하기가 어렵습니다. 무조
smartpro.tistory.com
2020/12/11 - [Algorithm] - [알고리즘] 백준 온라인 저지 사이트 - 문제 채점
[알고리즘] 백준 온라인 저지 사이트 - 문제 채점
지난 시간에 이어서 백준 온라인 저지 사이트 사용법을 알아보도록 하겠습니다. 문제 선택 및 풀이 연습삼아 간단한 코딩 문제 하나를 풀어보도록 하겠습니다. www.acmicpc.net/problem/1000 1000번: A+B
smartpro.tistory.com
'알고리즘' 카테고리의 다른 글
| [백준/1012/Java] 유기농 배추 - BFS 풀이 (0) | 2021.02.09 |
|---|---|
| [백준/1260/Java] DFS와 BFS (0) | 2021.02.07 |
| [백준/1325/Java] 효율적인 해킹 - BFS/DFS 풀이 (1) | 2021.02.01 |
| [백준/2178/Java] 미로탐색 - BFS 풀이 (0) | 2021.01.29 |
| [백준/7576/Java] 토마토 - BFS 풀이 (0) | 2021.01.28 |