2021. 2. 19. 22:47ㆍ알고리즘

문제
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net
문제를 먼저 풀고 오시는 것을 추천합니다.
이 문제의 풀이는 다익스트라(Dijkstra) 알고리즘 풀이 외에도 다양한 방법이 있을 수 있으며 제가 보여드리는 풀이는 그 중 하나입니다.
문제분석
시작점에서 갈 수 있는 모든 정점을 찾아야 합니다.
각 정점까지의 최단경로의 경로값을 구합니다. 즉, 각 정점까지의 가중치 합이 가장 최소로 되는 값을 구합니다.
그러므로 시작점에서 갈 수 있는 모든 정점에 대한 간선 및 가중치를 비교하되 최단경로 배열에 가장 작은 값을 저장하면 됩니다. 동적계획법(Dynamic Programming)의 메모이제이션을 활용하여 최단경로 min값을 비교하여 저장합니다.
단, 최단경로 배열은 초기값으로 INF (Integer.MAX_VALUE)로 설정합니다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어집니다. (1 <= V < 20,000, 1 <= E <= 300,000)
둘째 줄에는 시작정점의 번호 K(1 <= K <= V)가 주어집니다.
셋째 줄부터 E개의 줄에 걸쳐 세 개의 정수 (u, v, w)가 순서대로 주어집니다. u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻입니다.
출력
첫째 줄부터 i번째 줄에 i번 정점으로의 최단경로의 경로값을 출력합니다.
시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력합니다.
풀이
간선 정보는 단방향이므로 인접리스트로 저장합니다.
최단경로를 구하기 위하여 다익스트라(Dijkstra) 알고리즘을 사용하고 가중치가 작은 간선부터 손쉽게 구하기 위하여 우선순위 큐를 사용합니다.
예제풀이
백준 문제에 있는 예제로 어떻게 동작하는지 알아보도록 하겠습니다.
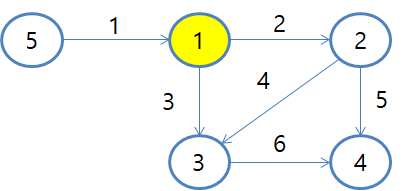
입력받은 5개의 정점, 6개의 간선을 그래프로 그려보았습니다.
시작정점은 노란색으로 표시한 1번 노드입니다.
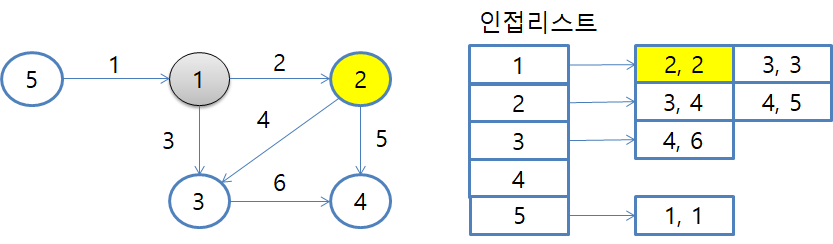
입력받은 정점 및 간선을 인접리스트로 저장하면 이렇게 저장됩니다.
인접리스트에 저장할 때 (정점번호, 가중치)의 형태로 저장합니다.

최단경로 배열 초기값은 모두 INF로 설정합니다. 시작정점인 1번 노드는 0을 설정합니다.

첫번째
1번 노드에서 2번 노드로 연결된 간선이 있으므로 2번 노드로 이동합니다.
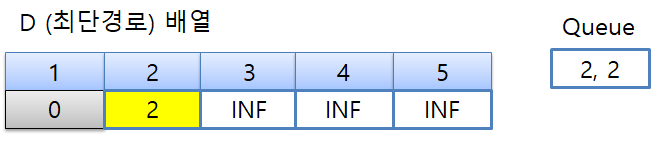
최단경로 배열에서 2번 노드에 저장되어 있는 INF와 2를 비교하면 2가 작기 때문에 D[2]에 2를 저장하고 우선순위 큐에 (2, 2)를 저장합니다.
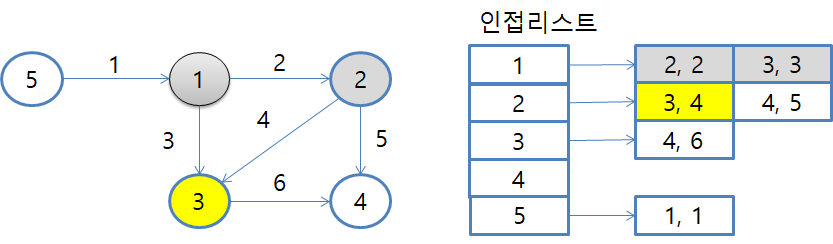
2번째
1번 노드에서 2번 노드로 연결된 남아있는 간선이 있으므로 3번 노드로 이동합니다.

최단경로 배열에서 3번 노드에 저장되어 있는 INF와 3를 비교하면 3이 작기 때문에 D[3]에 3을 저장하고 우선순위 큐에 (3, 3)을 넣습니다.

3번째
1번 노드에 연결된 모든 정점을 모두 돌았기 때문에 우선순위 큐에 있는 (2, 2)를 꺼냅니다.
2번 노드에서 연결된 3번 노드로 갑니다.
인접리스트에 있는 (3, 4)를 꺼내고 D[3] 값과 D[2]+가중치 4를 비교합니다.
D[3] < D[2] + 4
3 < 2+4
기존 D[3] 값이 더 작으므로 별다른 액션을 취하지 않습니다.

4번째
2번 노드로 연결된 남아있는 간선이 있으므로 4번 노드로 이동합니다.
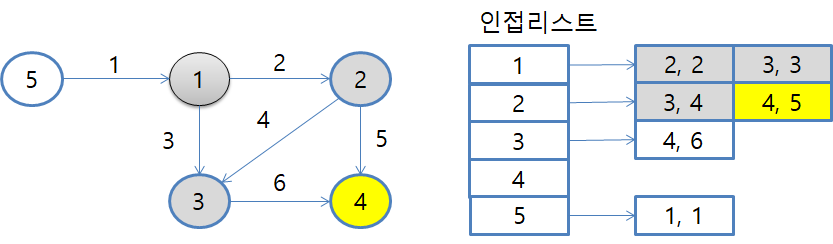
인접리스트에 있는 (4, 5)를 꺼내고 D[4] 값과 D[2]+가중치 5를 비교합니다.
D[4] < D[2] + 5
INF < 2+5
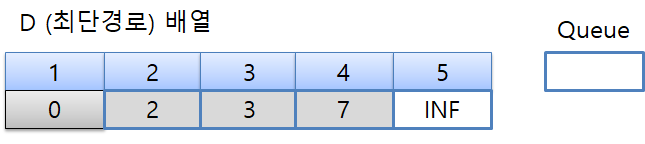
기존 D[2]+5 값이 7이므로 우선순위 큐에 4번 노드의 weight인 (4, 7)을 저장하고 최단경로 배열에도 7을 저장합니다.

5번째
우선순위 큐에 있는 (3,3)을 꺼내서 3번 노드로 이동합니다.
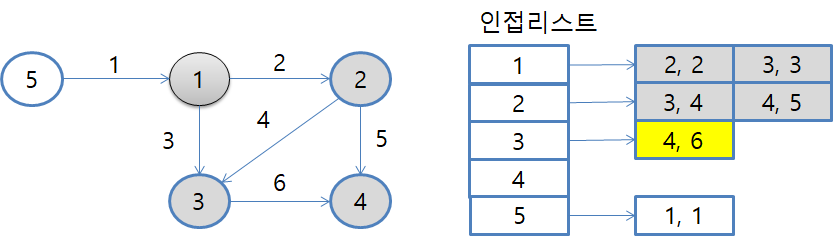
인접리스트에 있는 (4, 6)를 꺼내고 D[4] 값과 D[3]+가중치 6를 비교합니다.
D[4] < D[3] + 6
7 < 3+6
기존 D[4] 값이 더 작으므로 별다른 액션을 취하지 않습니다.
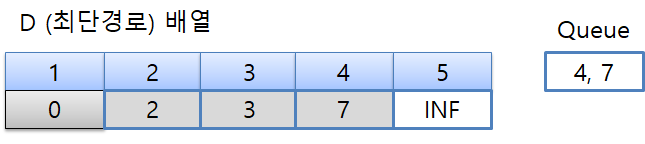
6번째
우선순위 큐에 있는 (4, 7)을 꺼내서 4번 노드로 이동합니다.
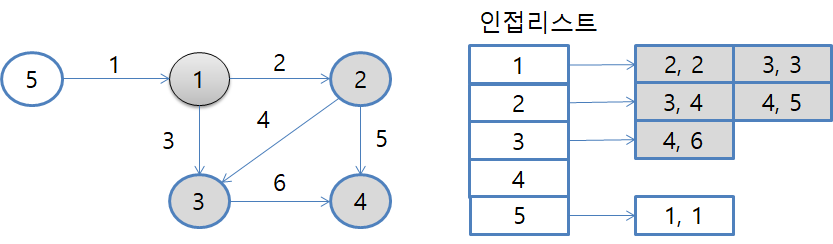
인접리스트에서 4번 노드에 연결된 것이 없으므로 별다른 액션을 취하지 않습니다.
큐에 남아있는 것이 없으므로 이대로 종료합니다.
소스
최단경로 배열인 D 배열을 꼭 INF인 Integer.MAX_VALUE로 초기화합니다.
다익스트라 알고리즘의 첫 시작정점은 입력받은 K로 합니다.
다익스트라 알고리즘은 우선순위 큐로 구현하며, D[다음노드], D[현재노드] + 다음노드에 연결된 간선의 가중치 중 낮은 값을 저장하도록 해야 합니다.
두 값이 같은 경우는 결과가 달라지지 않으므로 처리하지 않는 것이 속도에 좋습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main
{
static final int INF = Integer.MAX_VALUE;
static int V, E;
static int K;
static int[] D;
static List<Node>[] list;
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String input = br.readLine();
StringTokenizer st = new StringTokenizer(input);
V = Integer.valueOf(st.nextToken());
E = Integer.valueOf(st.nextToken());
input = br.readLine();
st = new StringTokenizer(input);
K = Integer.valueOf(st.nextToken());
D = new int[V+1];
Arrays.fill(D, INF); // INF로 초기화
list = new ArrayList[V+1];
for (int i = 1; i <= V; i++)
{
list[i] = new ArrayList<Node>();
}
for (int i = 0; i < E; i++)
{
input = br.readLine();
st = new StringTokenizer(input);
int u = Integer.valueOf(st.nextToken());
int v = Integer.valueOf(st.nextToken());
int w = Integer.valueOf(st.nextToken());
list[u].add(new Node(v, w));
}
dijkstra(K);
StringBuffer sb = new StringBuffer();
for (int i = 1; i <= V; i++)
{
if (D[i] == INF) sb.append("INF").append("\n");
else sb.append(D[i]).append("\n");
}
System.out.println(sb.toString());
}
private static void dijkstra(int start)
{
PriorityQueue<Node> q = new PriorityQueue<Node>();
q.add(new Node(start, 0));
D[start] = 0;
while (q.isEmpty() == false)
{
Node node = q.poll();
int c = node.v; // 현재 노드
for (Node t : list[c]) // 인접리스트에서 연결된 다음 노드를 가져온다.
{
if (D[t.v] > D[c] + t.w)
{
D[t.v] = D[c] + t.w;
q.add(new Node(t.v, D[t.v]));
// System.out.println("D : " + Arrays.toString(D));
// System.out.println(Arrays.toString(q.toArray()));
}
}
}
}
}
class Node implements Comparable<Node>
{
int v; // target Node
int w; // weight
Node(int v, int w)
{
this.v = v;
this.w = w;
}
@Override
public int compareTo(Node o)
{
return w - o.w;
}
@Override
public String toString()
{
return "{" + v + ", " + w + "}";
}
}
관련글:
2021/02/11 - [Algorithm] - 백준 온라인 저지 - 알고리즘 문제 난이도/유저 등급 확인하는 방법 (solved.ac)
백준 온라인 저지 - 알고리즘 문제 난이도/유저 등급 확인하는 방법 (solved.ac)
백준 온라인 저지에서 알고리즘 문제를 풀다보면 지금 풀고 있는 문제가 얼마나 어려운지 가늠하기 어려웠습니다. 그래서 맞은 사람, 제출, 정답비율을 보고 가늠하려고 하지만 쉽지 않았습니
smartpro.tistory.com
'알고리즘' 카테고리의 다른 글
| [백준/2146/Java] 다리 만들기 (0) | 2021.03.08 |
|---|---|
| [백준/2667/Java] 단지번호붙이기 (0) | 2021.03.05 |
| 백준 온라인 저지 - 알고리즘 문제 난이도/유저 등급 확인하는 방법 (solved.ac) (4) | 2021.02.11 |
| [백준/1012/Java] 유기농 배추 - BFS 풀이 (0) | 2021.02.09 |
| [백준/1260/Java] DFS와 BFS (0) | 2021.02.07 |